By Dr. Budhaditya Hazra, Liang Xu, and Dr. Suri Ganeriwala, SpectraQuest
With an increase in high-speed manufacturing and automation, it has become more important to use the theory of vibration for design and maintenance of machinery. This vibration theory is even more important in the monitoring and diagnosis of machinery malfunctions. Hence an effective manner of hands-on teaching of vibration principles is the need of the decade. However, most academic institutions include only theoretical lectures without laboratory exercises due a lack of an apparatus combined with an instrumentation setup. Keeping this chasm between industrial needs and academic output in mind, SpectraQuest has introduced a new innovative and modular bench scale experimental set-up called vibration fundamentals training system.
The Vibration Fundamentals Training system (alias VFT) is a turn-key integrated educational package for teaching/learning the fundamental principles of mechanical vibration as well as engineering mechanics. It provides both a comprehensive hands-on experimental device and an instrumentation package including wireless sensors for performing laboratory exercises to enhance student understanding of vibration theory. The VFT clearly brings classical theory to life by providing a convenient means to validate predictions and to demonstrate the influence of parameter changes on system response visually. Students can perform virtual experiments using the vibration simulation software and then verify the results with actual experiments thereby reinforcing the learning of difficult principles. The VFT provides an ideal tool for damping free vibration experiments using the wireless sensors without affected by the damping associated with the sensor cables. It is a perfect tool for teaching mechanical vibration courses both at under graduate and graduate levels.
In this technote, we present some of the very basic set of experiments that can be easily performed as a part of the vibration teaching curriculum. More advanced applications will be dealt later in subsequent tech notes.
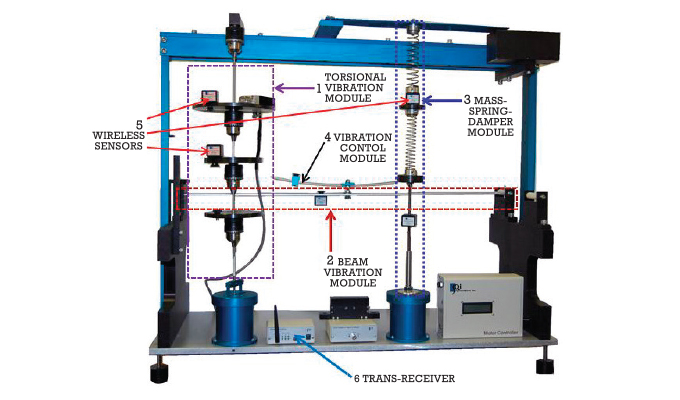
Figure 1 shows the VFT system with the basic modules, such as torsional vibration module, beam vibration module, spring-mass-damper system module, and vibration control module. Wireless accelerometers are used to collect data in the framework of a wireless data acquisition system. The data thus obtained is processed through SpectraQuest’s custom built software.
We now demonstrate the usage of the VFT system with the aid of a few simple experiments. The experiments are created in such a way that it can be used by any end-user to incorporate in a vibration teaching curriculum.
EXPERIMENT 1: DETERMINATION OF SPRING STIFFNESS
The basic step towards performing laboratory experiments to verify the fundamental concepts of vibration theory is to determine the spring stiffness or the stiffness constant. The most common practical problem is getting a massless spring. Mass springs merely facilitates theoretical development of single degree of freedom vibration equations. In reality, all springs have masses and the mass of the spring that participates in the SDOF vibration idealized as a lumped system is called the effective mass. The expression of effective mass is given in any standard textbooks and the readers are referred to some common works in this area.
In the first experiment, the stiffness constant of the spring is determined using both the static and the dynamic methods and verified with the theoretical expression obtained from the strength of materials background on close coiled helical springs.
OBJECTIVES
To determine the stiffness of a helical spring using two methods:
- Deflection curve and Hooke’s Law (static method).
- Natural frequency measurements of the SDOF mass-spring system (dynamic method).
Compare their results with the analytical value.

SYSTEM DESCRIPTION
The spring-mass system in figure 2 shows an extension linear helical spring with an initial free length Li, effective mass mS ( = 0.006 kg), supported vertically from one of its ends; while the other end is free to elongate and attached to a load carrier of (mC = 0.028 kg) mass. The free length of the spring loaded with the load carrier alone is LO.
Disks each of (m = 0.350Kg, 0.572Kg, 0.784Kg, and 0.920Kg) mass are added to the carrier gradually, and each loading state causes the spring to elongate by the distance from its unloaded length LO to get a total length of L.
GOVERNING EQUATIONS
For the spring-mass system shown in figure 2, in the case of free vibration in the vertical direction Y, the equation of motion of the system is given by
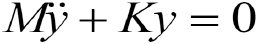
(where M is the total mass of the system, and equals to M = m + mC + mS). From the equation of motion, we can find that:
Natural frequency =
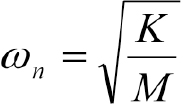
Period of oscillation =
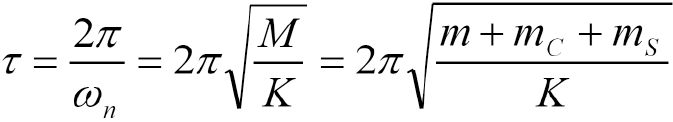
For the linear spring following Hooke’s law, then:
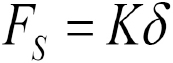
But for the present system, the spring force FS is also given by:
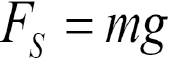
Combine these two equations to get:
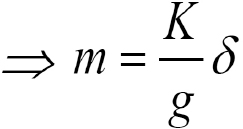
For a helical spring, the stiffness is expressed analytically as:
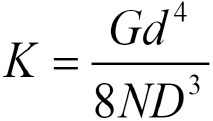
Using the dimensions of the spring as d = 0.062 inches, D = 0.938 inches, number of coils (N) = 17 and, torsional modulus G as 77.2 GPa, the theoretical value of stiffness comes out as
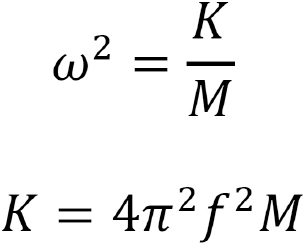
(where f is the natural frequency in hertz).

EXPERIMENTAL PROCEDURES
- Hang the spring vertically with the load carrier attached to its end, and then measure the total length of the spring LO (this length is not the initial free length of the spring Li).
- Add one disk to the carrier (m = md), and measure the total length of the spring after elongation L.
- Calculate the extension.
- With this loading, stretch the spring downward, then leave it to oscillate freely and record the natural frequency.
- Keep changing the disc mass to higher values (0.350Kg, 0.572Kg, 0.784Kg, and 0.920Kg) and repeat steps 1 to 4.
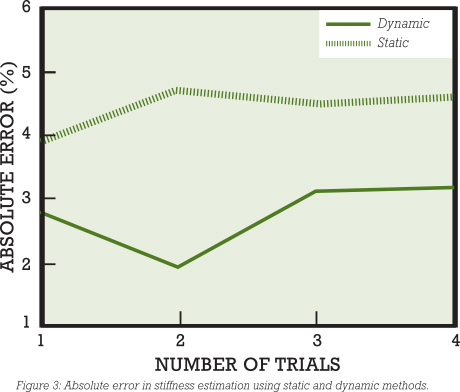
DATA PROCESSING
Figure 3 clearly shows that the errors in estimating stiffness is more using the static method compared to the dynamic method. However, for both the cases, the errors are less than 5 percent, which are within the acceptable limits for engineering applications.
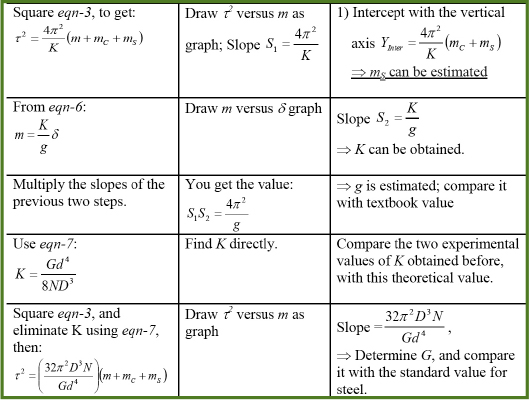
ADDITIONAL EXPERIMENTS BASED ON THE SAME WORKING PRINCIPLE
A few more experiments can also be performed based on the sample working principle. They are summarized briefly in Table 2.
A LOOK AHEAD
Generally speaking, vibratory systems consist basically of potential energy storing element (stiffness), kinetic energy storing element (mass or inertia), and energy dissipation element (damping). Damping effect in vibratory systems may be caused by friction between moving parts (dry friction), or material deformation and internal friction between layers of a part (structural action), or the use of mechanical viscous dampers. The first two may never be completely eliminated but can be, generally, ignored under certain conditions. However, the third can be used to achieve a required damping effect. In the experiments presented in next month’s conclusion to this series, we show that the damping contribution from dry friction and structural action is indeed negligible.
FOR MORE INFORMATION
SpectraQuest, Inc. is a leading developer and manufacturer of complete turn-key Systems for training and diagnosis in machine vibration analysis, rotor balancing, and shaft/coupling alignment. System includes machinery fault simulators, interactive training program, data acquisition hardware/software, and accessories. To accelerate the learning and design process SpectraQuest offers a series of interactive software CDs on vibration fundamentals and calculations, signal processing, alignment, and balancing. For more information, visit www.spectraquest.com.
MODERN PUMPING TODAY, February 2021
Did you enjoy this article?
Subscribe to the FREE Digital Edition of Modern Pumping Today Magazine!